Wprowadzenie
Aproksymacja polega na zastąpieniu funkcji $f$ inną funkcją $\bar{f}$, albo na wyznaczeniu funkcji $\bar{f}$ na podstawie określonego zbioru wartości funkcji $f$. Te wartości często mogą być obarczone znacznym błędem (wartości empiryczne). Funkcja aproksymująca $\bar{f}$ powinna być taka, by można było na niej łatwo przeprowadzać operacje matematyczne (różniczkowanie, całkowanie). Dlatego często stosuje się wielomiany algebraiczne, funkcje wymierne lub wielomiany trygonometryczne jako funkcje aproksymujące.
Źródła błędów w aproksymacji
W aproksymacji można wyróżnić dwa źródła błędów:
• dane wejściowe: błędy pomiarów.
• model (klasa funkcji): błędy wynikające z modelu, który ma być dopasowany do danych wejściowych.
W praktyce zarówno dane wejściowe, jak i sam model nie są idealne. Aproksymację można postrzegać jako problem dostosowania modelu matematycznego do dostępnych danych oraz innych znanych faktów.
Różnica między interpolacją a aproksymacją
Interpolacja polega na znajdowaniu funkcji, która dokładnie przechodzi przez wszystkie dane pomiarowe, zapewniając ścisłe dopasowanie w węzłąch interpolacji. Aproksymacja, z kolei, polega na znalezieniu funkcji, która najlepiej pasuje do danych w sensie minimalizacji błędu, niekoniecznie przechodząc przez wszystkie punkty.
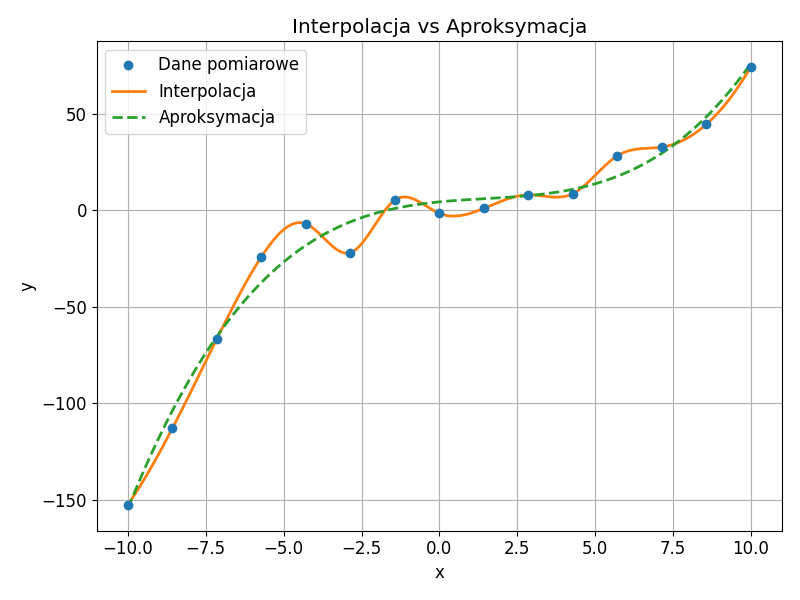
Interpolacja jest dokładniejsza w odniesieniu do danych wejściowych, ale może być wrażliwa na szum. Aproksymacja jest bardziej odporna na błędy pomiarowe i szum, oferując gładką i stabilną reprezentację danych. W praktyce, wybór metody zależy od specyfiki problemu i dokładności danych.
Regresja liniowa
Regresja liniowa to jedna z najprostszych technik analizy regresji, która służy do modelowania zależności liniowej pomiędzy zmienną niezależną a zmienną zależną. Zakłada się, że relacja między tymi zmiennymi jest liniowa, co oznacza, że można ją przedstawić za pomocą prostej linii.
Model regresji liniowej ma postać:
$$y=ax+b,$$gdzie $y$ to zmienna zależna, $x$ to zmienna niezależna, $a$ to współczynnik kierunkowy, a $b$ to wyraz wolny.
Celem regresji liniowej jest znalezienie wartości współczynników $a$ i $b$, które minimalizują sumę kwadratów różnic pomiędzy rzeczywistymi wartościami $y$ a wartościami przewidywanymi przez model.
Przykład:
Załóżmy, że mamy zbiór punktów $(x_i, y_i)$ i chcemy znaleźć linię regresji liniowej dla tych danych. Przyjmijmy, że nasze dane wyglądają następująco:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| y | 1 | 3 | 2 | 4 | 2 | 5 |
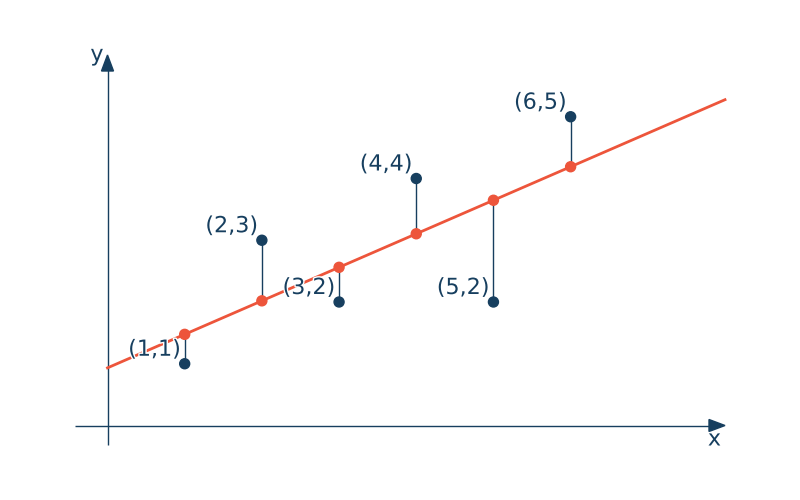
W pakiecie Scilab to wyznaczania prostej regresji służy funkcja reglin
[a,b]=reglin(x,y)
Argumentami tej funkcji są wektory zawierające współrzędne danych pomiarowych. Funkcja zwraca współczynniki opisujące równanie prostej.
# Przykład
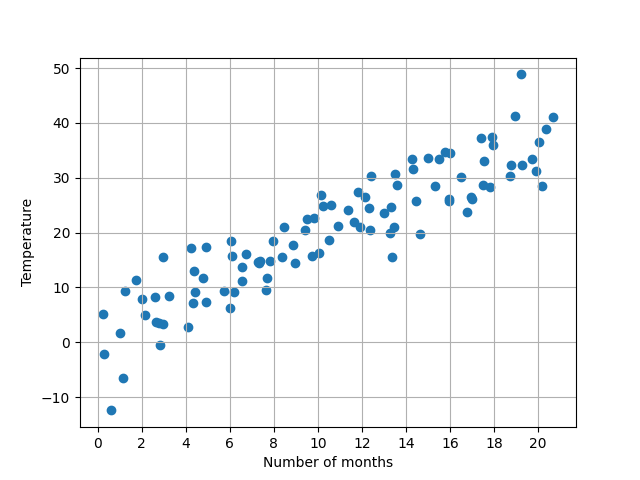
Na podstawie danych pomiarowych zapisanych w pliku oraz wbudowanej funkcji reglin() znaleźć równanie prostej regresji o równaniu $y = ax + b$, oraz przedstawić jej wykres wraz z punktami pomiarowymi.
// wczytanie danych z pliku
u = file('open','dane.txt','old')
A = read(u,-1,2);
file('close',u);
//obliczenie a i b krzywej regresji
[a,b]= reglin(A(:,1)',A(:,2)')
x = A(:,1); y = A(:,2)
yn=a*x+b
plot(x, yn, 'red')
plot(x, y, 'blackx')
Metoda najmniejszych kwadratów
Metoda najmniejszych służy do dopasowania funkcji (np. wielomianu) do zbioru danych w taki sposób, aby minimalizować sumę kwadratów odchyleń między obserwowanymi wartościami a wartościami przewidywanymi przez model. Zakłada się, że funkcja ma postać:
$$y = f(x, a_0, a_1, \dots, a_n),$$gdzie $ a_0, a_1, \dots, a_n $ to współczynniki modelu. Kryterium minimalizacji wyraża się wzorem:
$$S = \sum_{i=1}^m \left( y_i - f(x_i, a_0, a_1, \dots, a_n) \right)^2,$$Aby znaleźć współczynniki $ a_0, a_1, \dots, a_n $, należy rozwiązać układ równań normalnych, który wynika z zerowania pochodnych funkcji $ S $ względem każdego współczynnika. Wynik metody najmniejszych kwadratów zapewnia najlepsze dopasowanie modelu do danych w sensie minimalizacji błędu kwadratowego. Rówanie $MNK$ wygląda następująco
$$\A^T \A \cdot \a = \A^T \y,$$W metodzie najmniejszych kwadratów macierz $\A$ jest konstruowana w zależności od wybranej funkcji dopasowującej. Dla wielomianu stopnia $ n$:
$$y(x) = a_0 + a_1x + a_2x^2 + \dots + a_nx^n,$$macierz $ \A $ ma postać:
$$A = \begin{bmatrix} 1 & x_1 & x_1^2 & \dots & x_1^n \\ 1 & x_2 & x_2^2 & \dots & x_2^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_m & x_m^2 & \dots & x_m^n \end{bmatrix},$$# Przykład
// dane pomiarowe
x = linspace(-10, 10, 100);
y = 5 + 3*x + 2*x.^2 + 30*rand(1, 100)-15
//metoda najmnieszych kadratow
// y = ax^2 + bx + c
A = [ones(x'), x', x'.^2]
AT_A = A' * A
AT_y = A' * y'
c = AT_A \ AT_y;
disp(c);
x_fit = linspace(min(x), max(x), 500);
y_fit = c(1) + c(2)*x_fit + c(3)*x_fit.^2;
plot(x,y,"rs")
plot(x_fit, y_fit, 'b', 'LineWidth', 2)
# Przykład
Znajdź współczynniki $a$, $b$ i $c$ funkcji aproksymującej postaci
$$y = a\cdot x + b\cdot \sin(3x) + c \cdot \exp(x)$$z wykorzystaniem metody najmniejszych kwadratów, która opisuje zbiór danych pomiarowych zawartych w pliku .