Wprowadzenie

Płaskie konstrukcje inżynierskie to takie elementy, w których dominują dwa wymiary (długość i szerokość) w porównaniu do trzeciego (grubości). Przykładami takich konstrukcji są płyty, ściany, ściany oporowe, powłoki, czy różnego rodzaju pokrycia i przegrody. W inżynierii są one często analizowane w ujęciu dwuwymiarowym, co znacznie upraszcza obliczenia

Przy obliczeniach konstrukcji płaskich korzysta się z koncepcji płaskiego stanu naprężenia oraz płaskiego stanu odkształcenia. Są to dwa podstawowe modele wykorzystywane do uproszczenia rzeczywistych trójwymiarowych problemów wytrzymałościowych do analizy w dwóch wymiarach, co pozwala efektywniej i precyzyjniej wyznaczyć kluczowe parametry konstrukcyjne.

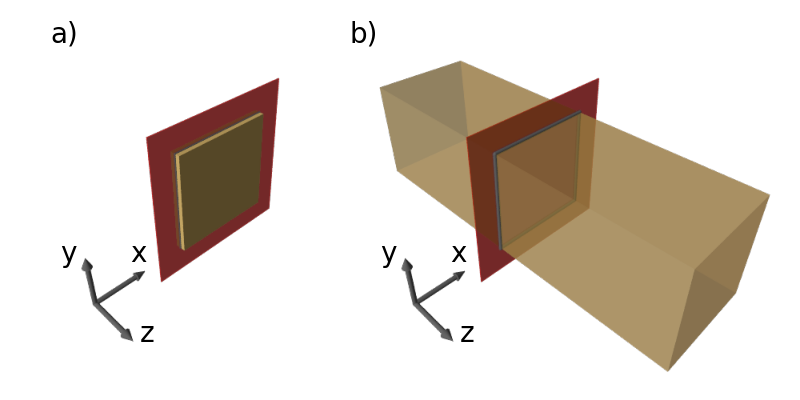
Płaski stan naprężenia

Płaski stan naprężenia odnosi się do sytuacji, w której obciążenie oraz wynikające z niego naprężenia występują w jednej płaszczyźnie (np. XY), podczas gdy naprężenie w kierunku trzecim (np. osi Z) jest zaniedbywalne lub bliskie zeru. Oznacza to, że wektor naprężeń ma komponenty jedynie w dwóch kierunkach, co znacznie upraszcza analizę. Ten model jest szczególnie przydatny przy analizie cienkich elementów płaskich poddanych obciążeniom w ich płaszczyźnie, np. cienkich płyt i membran.

$$\ss = \mat{ \sigma_{11} }{ \sigma_{12} }{ \sigma_{13} }{ \sigma_{21} }{ \sigma_{22} }{ \sigma_{23} }{ \sigma_{31} }{ \sigma_{32} }{ \sigma_{33} }= \mat{ \sigma_{11} }{ \sigma_{12} }{ 0 }{ \sigma_{21} }{ \sigma_{22} }{ 0 }{ 0 }{ 0 }{ 0 }\quad \rightarrow \quad \ss = \matt{ \sigma_{11} }{ \sigma_{12} }{ \sigma_{21} }{ \sigma_{22} }$$

Założenia dla płaskiego stanu naprężenia:
• Naprężenie w kierunku prostopadłym do płaszczyzny jest bliskie zeru ($\sigma_{33}=0$).
• Obciążenia i przemieszczenia działają jedynie w płaszczyźnie, a wpływ obciążenia w trzecim kierunku jest pomijalny.
• Grubość elementu jest na tyle mała, że efekty wynikające z jej zmienności nie mają znaczącego wpływu na rozkład naprężeń.

Płaski stan odkształcenia

Płaski stan odkształcenia występuje wtedy, gdy odkształcenia w trzecim kierunku są pomijalne (np. odkształcenia w osi Z są zerowe). Zwykle stosuje się go w sytuacjach, gdy konstrukcja jest na tyle gruba, że odkształcenia w kierunku prostopadłym do analizowanej płaszczyzny nie wpływają na rozkład naprężeń i odkształceń. Taki stan jest typowy dla konstrukcji masywnych, jak fundamenty czy elementy betonowe o dużych wymiarach w porównaniu do obszaru podlegającego analizie.

$$\ee = \mat{ \varepsilon_{11} }{ \varepsilon_{12} }{ \varepsilon_{13} }{ \varepsilon_{21} }{ \varepsilon_{22} }{ \varepsilon_{23} }{ \varepsilon_{31} }{ \varepsilon_{32} }{ \varepsilon_{33} }= \mat{ \varepsilon_{11} }{ \varepsilon_{12} }{ 0 }{ \varepsilon_{21} }{ \varepsilon_{22} }{ 0 }{ 0 }{ 0 }{ 0 }\quad \rightarrow \quad \ee = \matt{ \varepsilon_{11} }{ \varepsilon_{12} }{ \varepsilon_{21} }{ \varepsilon_{22} }$$

Założenia dla płaskiego stanu odkształcenia:
• Odkształcenie w kierunku prostopadłym do płaszczyzny $\varepsilon_{33}$ jest zaniedbywalne.
• W analizowanej płaszczyźnie występują jedynie dwa główne kierunki naprężeń i odkształceń.
Konstrukcja jest na tyle gruba, że wpływ odkształceń w trzecim wymiarze można pominąć w analizie.