Wprowadzenie

Teoria płyt Kirchhoffa-Love’a jest klasyczną teorią mechaniki ciągłej, która opisuje zachowanie cienkich płyt poddanych obciążeniom. Teoria ta wywodzi się z klasycznej teorii zginania belek opracowanej przez Leonharda Eulera i Daniela Bernoulliego w XVIII wieku. W połowie XIX wieku niemiecki matematyk Gustav Kirchhoff rozszerzył te idee na płyty, wprowadzając kluczowe założenia dotyczące zachowania się cienkich struktur w dwóch wymiarach. Kirchhoff zaproponował podstawowe równania opisujące równowagę cienkich płyt, a jego prace stały się fundamentem nowoczesnej teorii płyt. Pod koniec XIX wieku Augustus Edward Hough Love, brytyjski matematyk, dokonał dalszego rozwinięcia tej teorii, wprowadzając bardziej formalne podejście matematyczne.

Model fizyczny

Płyta cienka jest modelowana jako powierzchnia środkowa, która znajduje się w połowie grubości rzeczywistej płyty. Powierzchnia środkowa jest abstrakcyjnym odwzorowaniem geometrycznym płyty i służy do uproszczenia analizy.

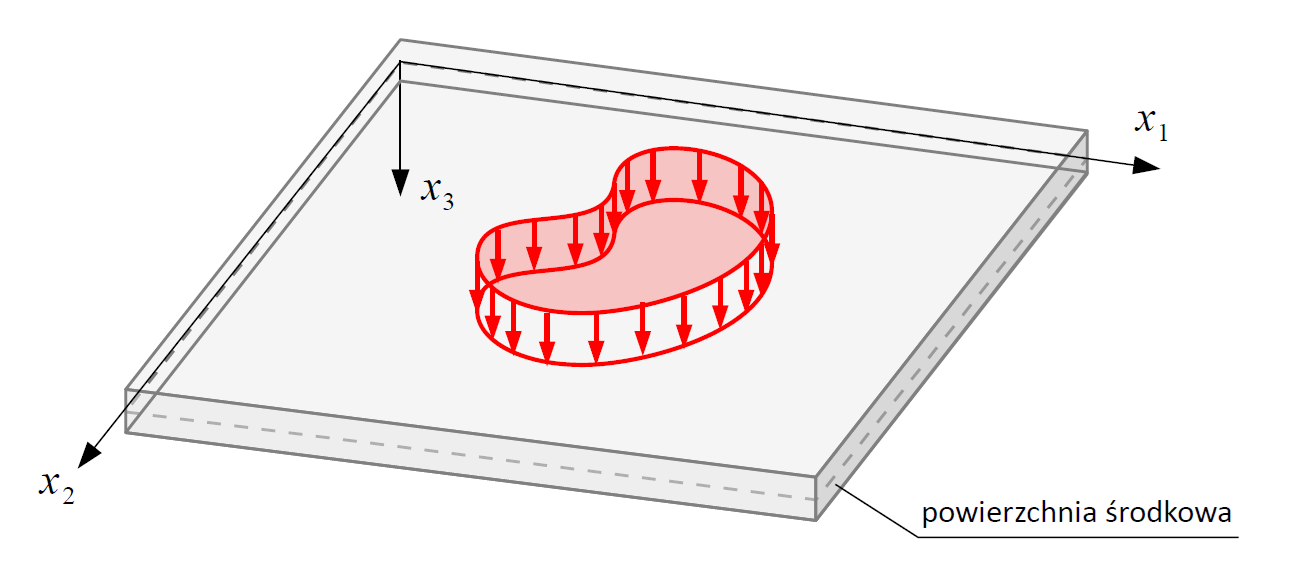
Płyta obciążona jest prostopadle do swojej powierzchni środkowej.

Założenie

Teoria Kirchhoffa-Love'a zakłada kilka istotnych uproszczeń:

• Geometria cienkiej płyty:

Płyta jest cienka, co oznacza, że stosunek grubości $h$ do innych wymiarów (długości i szerokości jest bardzo mały:

• Hipoteza płaskich przekrojów:

Odcinek prosty i prostopadły do płaszczyzny środkowej płyty przed deformacją
pozostaje prosty i prostopadły do zdeformowanej powierzchni środkowej płyty

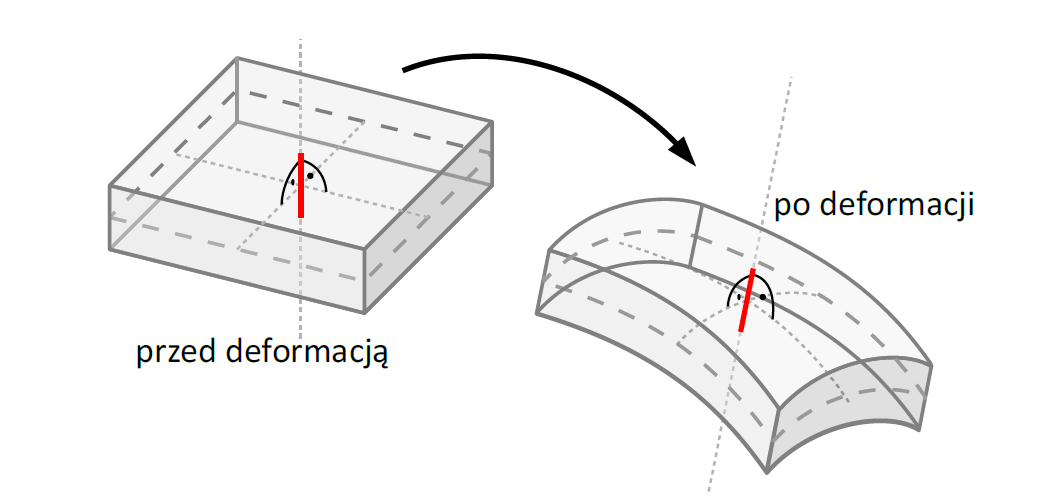
Po deformacji płyty przekroje poprzeczne, które były prostopadłe do powierzchni środkowej przed deformacją, pozostają płaskie i prostopadłe do powierzchni środkowej po deformacji.

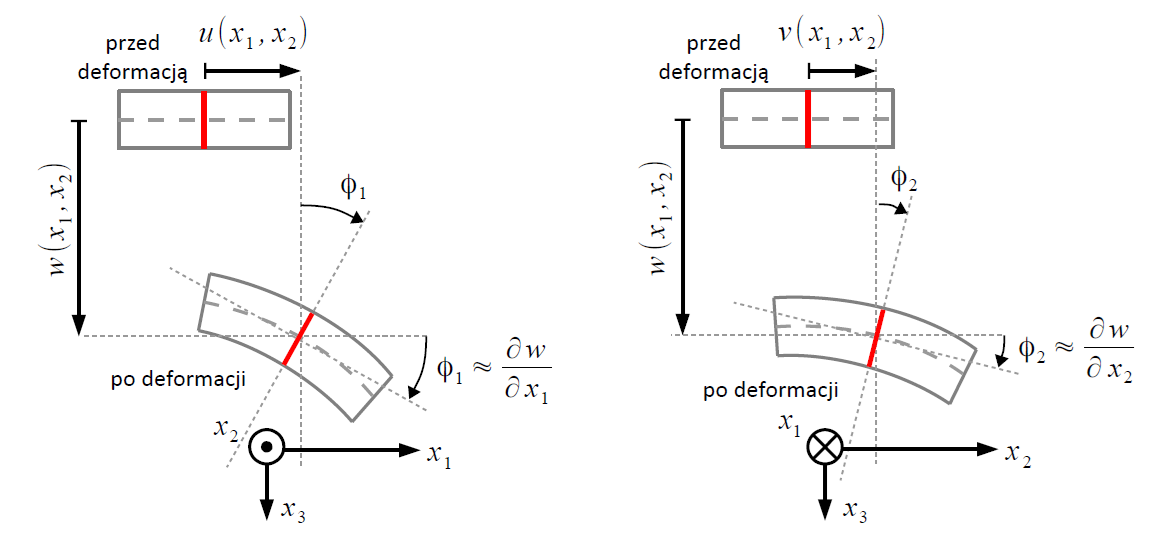
• Zakłada się brak odkształceń ścinających w kierunku grubości, co oznacza, że deformacje poprzeczne są pomijalne.

• Płyta doświadcza wyłącznie małych odkształceń, co pozwala na liniowe przybliżenie związków między naprężeniami a odkształceniami. Przemieszczenie w kierunku osi $z$ (prostopadłym do powierzchni płyty) jest dominujące w porównaniu do przemieszczeń w płaszczyźnie

• Materiał płyty spełnia liniowe prawo Hooke’a, co pozwala opisać naprężenia w płycie za pomocą modułu Younga $E$ oraz współczynnika Poissona $\nu$.

• Naprężenia normalne prostopadłe do powierzchni środkowej płyty są pomijalnie małe $\sigma_{33}=0$.

• Równowaga sił i momentów: Płyta znajduje się w równowadze mechanicznej, uwzględniającej siły wewnętrzne (rozciągające i zginające) oraz obciążenia zewnętrzne.

Model matematyczny

Zakłada się, że przemieszczenie w kierunku osi $z$ można zapisać jako $w(x_1, x_2)$. Równowaga mechaniczna płyty w kierunku osi $z$ z prowadzi do równania różniczkowego czwartego rzędu:

$$\pp{^4 w(x_1,x_2)}{x_1^4} + 2\pp{^4 w(x_1,x_2)}{x_1^2 \partial x_2^2} + \pp{^4 w(x_1,x_2)}{x_2^4} = \cfrac{q(x_1,x_2)}{D}$$

gdzie $q(x_1,x_2)$ to zewnętrzne obciążenie działające na powierzchnię płyty $[N/m^2]$, a $D$ opisuje sztywność giętną płyty wyrażone zależnością

$$D = \cfrac{Eh^3}{12(1-\nu^2)}$$

Warunki brzegowe:
Równania muszą być uzupełnione odpowiednimi warunkami brzegowymi, które mogą obejmować:
• warunki podporowe (np. swobodne, utwierdzone, przegubowe),
• warunki naturalne wynikające z momentów i sił brzegowych.